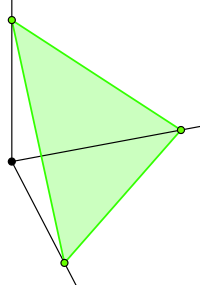
Симплекс

Запрос «Симплекс» перенаправляется сюда; см. также другие значения.

Симплекс или n-мерный тетраэдр (от лат. simplex — простой) — геометрическая фигура, являющаяся n-мерным обобщением треугольника.

Определение

Симплекс есть выпуклая оболочка n+1 точек, не лежащих в одной гиперплоскости n-мерного Евклидова пространства. Эти точки называются вершинами симплекса.

Связанные определения

• Симплекс называется правильным, если все его рёбра имеют одинаковую длину.

Стандартный симплекс

Зелёный треугольник — стандартный 2-симплекс

Стандартный n-симплекс это подмножество $\mathbb{R}^{n+1}$, определяемое как:

$\Delta^n=\{(t_0,\dots, t_n)\mid {(\sum_i t_i = 1)} \wedge {(\forall i \; t_i\geqslant 0)} \}.$

Его вершинами являются точки:

e₀=(1, 0, …, 0),

e₁=(0, 1, …, 0),

…

e_n=(0, 0, …, 1).

Существует каноническое взаимно-однозначное отображение стандартного n-симплекса в любой другой n-симплекс с координатами вершин $(v_0, v_1,\dots, v_n)$:

$(t_0,\dots, t_n) \mapsto \sum_i t_i v_i.$

Значения t_i для данной точки называются её барицентрическими координатами.

Свойства

• n-мерный симплекс имеет $n+1$ вершин, любые $k+1$ из которых образуют k-мерную грань.
  • В частности, число k-мерных граней в n-симплексе равно биномиальному коэффициенту $\tbinom{n+1}{k+1}.$
  • В частности, число граней старшей размерности совпадает с количеством вершин и равно $n+1$.
• Ориентированный объём n-симплекса в n-мерном евклидовом пространстве можно определить по формуле:

  $V=\frac{1}{n!} \det(v_1-v_0, v_2-v_0, \dots, v_n-v_0)$

  • Определитель Кэли — Менгера позволяет вычислить объём симплекса, зная длины его рёбер:

    $V^2 = \frac{(-1)^{n-1}}{2^n (n!)^2} \begin{vmatrix} 0 & 1 & 1 & 1 & \dots & 1 \\ 1 & 0 & d_{01}^2 & d_{02}^2 & \dots & d_{0n}^2 \\ 1 & d_{10}^2 & 0 & d_{12}^2 & \dots & d_{1n}^2 \\ 1 & d_{20}^2 & d_{21}^2 & 0 & \dots & d_{2n}^2 \\ \vdots&\vdots&\vdots & \vdots & \ddots& \vdots \\ 1 & d_{n0}^2 & d_{n1}^2 & d_{n2}^2 & \dots & 0 \\ \end{vmatrix}$

где $d_{ij}=|v_i - v_j|$ — расстояние между i-й и j-й вершинами, n — размерность пространства. Эта формула является обобщением формулы Герона для треугольников.

• Объём правильного n-симплекса с единичной стороной равен $\frac{\sqrt{n+1}}{n!\cdot 2^{n/2}}.$

• Радиус $R$ описаной n-мерной сферы удовлетворяет соотношению

  $(R{\cdot}V)^2=T,$

где $V$-объем симплекса и

$T = \frac{(-1)^{n}}{2^{n+1}{n!}^2} \begin{vmatrix} 0 & d_{12}^2 & d_{13}^2 & \dots & d_{1(n+1)}^2 \\ d_{21}^2 & 0 & d_{23}^2 & \dots & d_{2(n+1)}^2 \\ d_{31}^2 & d_{32}^2 & 0 & \dots & d_{3(n+1)}^2 \\ \vdots&\vdots & \vdots & \ddots&\vdots& \\ d_{(n+1)1}^2 & d_{(n+1)2}^2 & d_{(n+1)3}^2 & \dots & 0 \\ \end{vmatrix}$

Построение

Преобразование 1-симплекса в 2-симплекс

Преобразование 2-симплекса в 3-симплекс

Через любые n точек можно провести (n–1)–плоскость и существуют множества из n+1 точек, через которые (n–1)–плоскость провести нельзя. Таким образом, n+1 — минимальное число точек в n–пространстве, которое не лежит в одной (n–1)–плоскости, и может служить вершинами n–многогранника.

Простейший n–многогранник с количеством вершин n+1 называется симплексом. Принято также название «n-мерный тетраэдр». В пространствах низшей размерности этому определению соответствуют 4 фигуры:

• 0-симплекс (точка) – 1 вершина;
• 1–симплекс (отрезок) – 2 вершины;
• 2–симплекс (треугольник) – 3 вершины;
• 3–симплекс (тетраэдр) – 4 вершины.

Все эти фигуры обладают тремя общими свойствами:

1. В соответствии с определением, число вершин у каждой фигуры на единицу больше размерности пространства;
2. Существует общее правило преобразования фигур низшей размерности в фигуры высшей размерности. Оно заключается в том, что из геометрического центра фигуры строится перпендикуляр в следующее измерение, на этом перпендикуляре строится новая вершина и соединяется рёбрами со всеми вершинами исходного симплекса;
3. Как следует из описанной в п. 2 процедуры, любая вершина симплекса соединена рёбрами со всеми остальными вершинами.

Описанная сфера

Построение описанной 2-сферы вокруг 1-симплекса с дополнительной точкой

Вокруг любого n-симплекса можно описать n-сферу.

Для 1-симплекса это утверждение очевидно. Описанная 1-сфера будет представлять собой отрезок, совпадающий с самим 1-симплексом, и её радиус будет составлять R = a/2. Добавим к 1-симплексу ещё одну точку и попробуем описать вокруг них 2-сферу.

Построим 2-сферу s₀ радиусом a/2 таким образом, чтобы отрезок AB был её диаметром. Если точка С находится за пределами окружности s₀, то увеличивая радиус окружности и смещая её в сторону точки С можно добиться того, что все три точки окажутся на окружности. Если же точка С лежит внутри окружности s₀, то подогнать окружность под эту точку можно увеличивая её радиус и смещая в сторону, противоположную точке С. Как видно из рисунка, сделать это можно в любом случае, когда точка С не лежит на одной прямой с точками АВ. Не является помехой и несимметричное расположение точки С относительно АВ.

Рассматривая общий случай, предположим, что существует (n–1)-сфера S_n-1 радиуса r, описанная вокруг некоторой (n–1)-мерной фигуры. Поместим центр сферы в начало координат. Уравнение сферы будет иметь вид

$x_1^2+x_2^2+x_3^2+ ... + x_{n-1}^2 = r^2. \qquad (1)$

Построим n-сферу с центром в точке (0, 0, 0, ... 0, h_S) и радиусом R, причём

$R^2=r^2+h_S^2.$

Уравнение этой сферы

$x_1^2+x_2^2+x_3^2+ ... + x_{n-1}^2+(x_n-h_S)^2 = r^2+h_S^2$

или

$x_1^2+x_2^2+x_3^2+ ... + x_{n-1}^2 = r^2-x_n^2+2x_nh_S. \qquad (2)$

Подставив в уравнение (2) x_n = 0, получим уравнение (1). Таким образом, при любом h_S сфера S_n-1 является подмножеством сферы S_n, а именно – её сечением плоскостью x_n = 0.

Предположим, что точка С имеет координаты (X₁, X₂, X₃, ..., X_n ). Преобразуем уравнение (2) к виду

$x_1^2+x_2^2+x_3^2+ ... + x_{n-1}^2 + x_n^2 = r^2+2x_nh_S$

и подставим в него координаты точки С:

$X_1^2+X_2^2+X_3^2+ ... + X_{n-1}^2 + X_n^2 = r^2+2X_nh_S.$

Выражение в левой части представляет собой квадрат расстояния R_C от начала координат до точки C, что позволяет привести последнее уравнение к виду

$R_C^2 = r^2+2X_nh_S,$

откуда можно выразить параметр h_S:

$h_S = \frac{R_C^2-r^2}{2X_n}.$

Очевидно, что h_S существует при любых R_C, X_n и r, кроме X_n = 0. Это значит, что если точка С не лежит в плоскости сферы S_n–1, всегда можно найти такой параметр h_S, что на сфере S_n c центром (0, 0, 0, ..., h_S) будет лежать и сфера S_n–1, и точка С. Таким образом, вокруг любых n+1 точек можно описать n–сферу, если n из этих точек лежат на одной (n–1)–сфере, и последняя точка не лежит с ними в одной (n–1)–плоскости.

Применяя последнее по индукции, можно утверждать, что n–сферу можно описать вокруг любых n+1 точек, если они не лежат в одной (n–1)–плоскости.

Число граней симплекса

Симплекс имеет n+1 вершин, каждая из которых соединена рёбрами со всеми остальными вершинами.

Поскольку все вершины симплекса соединены между собой, то тем же свойством обладает и любое подмножество его вершин. Это значит, что любое подмножество из L+1 вершин симплекса определяют его L–мерную грань, и эта грань сама является L–симплексом. Тогда для симплекса число L-мерных граней равно числу способов выбрать L+1 вершину из полного набора n+1 вершин.

Обозначим символом К(L,n) число L–мерных граней в n–многограннике, тогда для n-симплекса

$K(L,n) = C^{L+1}_{n+1},$

где $C^m_n$ – число сочетаний из n по m.

В частности, число граней старшей размерности равно числу вершин и равно n+1:

$K(0,n) = K(n-1,n) = n+1.$

Соотношения в правильном симплексе

В правильном n-мерном симплексе со стороной $a$ пусть

• $H_n$ обозначает высоту,
• $V_n$ обозначает объём,
• $R_n$ обозначает радиус описанной сферы,
• $r_n$ обозначает радиус вписанной сферы.
• $\alpha_n$ обозначает двугранный угол,

Тогда

• $H_n = a\sqrt{\frac{n+1}{2n}}= R_n \frac{n+1}{n}$
• $V_n = \frac{a^n}{n!}\sqrt{\frac{n+1}{2^n}}= \frac{R^n_n}{n!} \sqrt{\left( \frac{n+1}{n} \right)^n}$
• $R_n = a\sqrt{\frac{n}{2(n+1)}}$
• $r_n = \frac{a}{\sqrt{2n(n+1)}}= \frac{R_n}{n}$
• $\cos \alpha = \frac{1}{n}$
• $R_n = H_n \frac{n}{n-1}$
• $a^2 = H_n^2 + R_{n-1}^2$
• $V_n = \frac{1}{n}V_{n-1}H_n$
• $r_n = R_n^2 - R_{n-1}^2$

Формулы для правильного симплекса

Число L-мерных граней	$K(L,n) = \tbinom{n+1}{L+1}$
Высота	$H_n = a\sqrt{\frac{n+1}{2n}}$	$H_n = R_n \frac{n+1}{n}$	$H_2 = a \frac{\sqrt{3}}{2}$	$H_3 = a \frac{\sqrt{6}}{3}$	$H_4 = a \frac{\sqrt{10}}{4}$
Объём	$V_n = \frac{a^n}{n!}\sqrt{\frac{n+1}{2^n}}$	$V_n = \frac{R^n_n}{n!} \sqrt{\left( \frac{n+1}{n} \right)^n}$	$V_2 = a^2 \frac{\sqrt{3}}{4}$	$V_3 = a^3 \frac{\sqrt{2}}{12}$	$V_4 = a^4 \frac{\sqrt{5}}{96}$
Радиус описанной сферы	$R_n = a\sqrt{\frac{n}{2(n+1)}}$	$a = R_n \sqrt{\frac{2(n+1)}{n}}$	$R_2 = a \frac{\sqrt{3}}{3}$	$R_3 = a \frac{\sqrt{6}}{4}$	$R_4 = a \frac{\sqrt{10}}{5}$
Радиус вписанной сферы	$r_n = \frac{a}{\sqrt{2n(n+1)}}$	$r_n = \frac{R_n}{n}$	$r_2 = a \frac{\sqrt{3}}{6}$	$r_3 = a \frac{\sqrt{6}}{12}$	$r_4 = a \frac{\sqrt{10}}{20}$
Двугранный угол	$\cos \alpha = \frac{1}{n}$

Литература

• Александров П. С., Комбинаторная топология, М. — Л., 1947
• Понтрягин Л. С., Основы комбинаторной топологии, М. — Л., 1947, с. 23—31.

См. также

• Барицентрическое подразделение
• Симплекс-метод
• Симплициальный комплекс
• N-мерная евклидова геометрия
• Теорема косинусов
• Сумма углов треугольника

Ссылки

• БСЭ — Симплекс