- Ковариантное дифференцирование
-
Ковариантная производная — обобщение понятия производной для тензорных полей на многообразиях. Понятие ковариантной производной тесно связано с понятием аффинной связности.
Ковариантная производная тензорного поля T в направлении касательного вектора
 обычно обозначается
обычно обозначается  .
.Содержание
Формальное определение
Скалярные функции
Для скалярной функции f ковариантная производная
 совпадает с обычной производной функции по направлению векторного поля
совпадает с обычной производной функции по направлению векторного поля 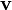 .
.Векторные поля
Ковариантная производная
 векторного поля
векторного поля  по направлению векторного поля
по направлению векторного поля  , обозначаемая
, обозначаемая  определяется по следующим свойствам, для любого вектора
определяется по следующим свойствам, для любого вектора 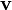 , векторных полей
, векторных полей 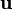 ,
,  и скалярных функций f и g:
и скалярных функций f и g: линейно по отношению к
линейно по отношению к  , то есть
, то есть 
 аддитивно относительно
аддитивно относительно  , то есть
, то есть 
 подчиняется правилу произведения, то есть
подчиняется правилу произведения, то есть  где
где  определено выше.
определено выше.
Замечание
Заметим, что
 в точке p зависит только от значения
в точке p зависит только от значения 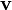 в точке p и от значений
в точке p и от значений 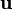 в ее окрестности. В частности, оператор ковариантной производной не является тензором (несмотря на то, что его значение на каждом тензорном поле тензором является).
в ее окрестности. В частности, оператор ковариантной производной не является тензором (несмотря на то, что его значение на каждом тензорном поле тензором является).Ковекторные поля
Если задано поле ковекторов (или 1-форм) α, его ковариантная производная
 может быть определена используя следующее тождество, которое удовлетворяется для всех векторных полей
может быть определена используя следующее тождество, которое удовлетворяется для всех векторных полей 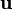
Ковариантная производная ковекторного поля вдоль векторного поля
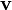 — тоже ковекторное поле.
— тоже ковекторное поле.Тензорные поля
Как только ковариантная производная определена для векторных и ковекторных полей, ее легко обобщить на произвольные тензорные поля при помощи правила Лейбница (
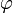 и ψ — произвольные тензоры):
и ψ — произвольные тензоры):Если
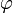 и ψ — тензорные поля из одного и того же тензорного расслоения, их можно сложить:
и ψ — тензорные поля из одного и того же тензорного расслоения, их можно сложить:Выражение в координатах
Пусть тензорное поле типа (p,q) задано своими компонентами
 в некоторой локальной системе координат xk, причем компоненты — дифференцируемые функции. Тогда ковариантная производная тензорного поля представляет собой тензор типа (p,q + 1), который определяется по формуле:
в некоторой локальной системе координат xk, причем компоненты — дифференцируемые функции. Тогда ковариантная производная тензорного поля представляет собой тензор типа (p,q + 1), который определяется по формуле:
где Γkij — символы Кристоффеля, выражающие связность искривленного многообразия.
Примеры для некоторых типов тензорных полей
Ковариантная производная векторного поля
 имеет по сравнению с частной производной дополнительное слагаемое,
имеет по сравнению с частной производной дополнительное слагаемое,Ковариантная производная скалярного поля
 совпадает с частной производной,
совпадает с частной производной,а ковариантная производная ковекторного поля
 -
-В пространстве без кручения символы Кристоффеля симметричны, и ковариантные производные скалярного поля коммутируют:
В общем случае ковариантные производные тензоров не коммутируют (см. тензор кривизны).
Ковариантная производная тензорного поля типа (2,0)
 равна
равнато есть
Для тензорного поля с одним верхним, одним нижним индексом ковариантная производная равна
наконец, для дважды ковариантного тензорного поля, то есть поля типа (0,2),
См. также
- Тензор кривизны
- Связность Леви-Чивиты
- Символы Кристоффеля
- Оператор набла в различных системах координат
Wikimedia Foundation. 2010.











