- Символы Кристоффеля
-
Символы Кристоффеля являются координатными выражениями аффинной связности, в частности связности Леви-Чивиты. Названы в честь Элвина Бруно Кристоффеля (1829—1900),
Символы Кристоффеля используются в дифференциальной геометрии, общей теории относительности и близких к ней теориях гравитации.
Символы Кристоффеля появляются в координатном выражении тензора кривизны. При этом сами символы тензорами не являются.
Ниже используется правило суммирования Эйнштейна, то есть по повторяющимся индексам подразумевается суммирование.
Содержание
Элементарное понятие о символах Кристоффеля
Введение
Наглядное представление о символах Кристоффеля можно получить на примере полярной системы координат. В этой системе координатами точки являются расстояние
 от неё до полюса и угол
от неё до полюса и угол  направления от полярной оси.
направления от полярной оси.Координатами вектора, как и в прямоугольной системе координат, следует считать дифференциалы (бесконечно малые приращения) этих величин:
 .
.Пусть есть вектор
 с координатами
с координатами  , где
, где  имеет геометрический смысл проекции вектора
имеет геометрический смысл проекции вектора  на радиальный луч (проходящий через начало вектора), а
на радиальный луч (проходящий через начало вектора), а  — угол, под которым вектор виден из полюса.
— угол, под которым вектор виден из полюса.В прямоугольной системе координат компоненты вектора не меняются при параллельном переносе. В полярной системе координат это не так (см. рисунки). Символы Кристоффеля как раз и выражают изменение компонент вектора при его параллельном переносе.
Параллельный перенос вдоль координатных линий
При смещении вектора вдоль радиального луча на расстояние
 , его компонента
, его компонента  , очевидно, не меняется, но вторая его координата (
, очевидно, не меняется, но вторая его координата ( ) уменьшается (рис. 1). Величина вектора
) уменьшается (рис. 1). Величина вектора  остаётся неизменной, поэтому
остаётся неизменной, поэтому  . Отсюда получается (пренебрежением величинами второго и большего порядков малости):
. Отсюда получается (пренебрежением величинами второго и большего порядков малости):
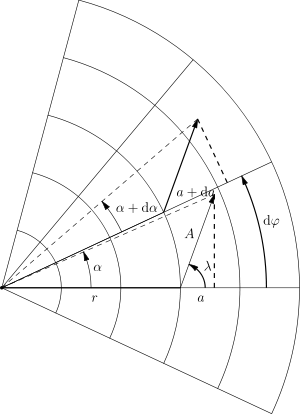
При параллельном переносе вдоль дуги меняются обе координаты
 и
и  (рис. 2). Очевидно,
(рис. 2). Очевидно,  ,
,  , и
, и  поэтому:
поэтому:
Кроме этого, так как
 ,
,  , и
, и  , то
, то
Параллельный перенос в произвольном направлении
При произвольном малом смещении вектора (когда меняются и
 , и
, и  ) изменения компонент надо складывать:
) изменения компонент надо складывать:

Полученные выражения имеют общую структуру: изменение компонент вектора пропорционально всем компонентам вектора и пропорционально величине сдвига вектора. Коэффициенты пропорциональности (без общего минуса) и называются символами Кристоффеля.
В более общих обозначениях
 ,
,  ,
,  и
и  можно записать (имея ввиду сумму по повторяющимся индексам):
можно записать (имея ввиду сумму по повторяющимся индексам):
Здесь символы Кристоффеля
 ,
,  , а все остальные равны нулю.
, а все остальные равны нулю.В прямоугольной системе координат все символы Кристоффеля равны нулю, так как компоненты вектора не изменяются при параллельном переносе. Из этого можно сделать вывод, что символы Кристоффеля не образуют тензор: если тензор равен нулю в какой-либо системе координат, то он равен нулю во всех остальных системах координат.
Символы Кристоффеля первого и второго рода
Символы Кристоффеля второго рода
 можно определить как коэффициенты разложения ковариантной производной координатных векторов
можно определить как коэффициенты разложения ковариантной производной координатных векторов  по базису:
по базису:Символы Кристоффеля первого рода

Выражение через метрический тензор
Символы Кристоффеля связности Леви-Чивита для карты
 могут быть определены из отсутствия кручения, то есть
могут быть определены из отсутствия кручения, то естьи того условия, что ковариантная производная метрического тензора
 равна нулю:
равна нулю:Для сокращения записи символ набла
 и символы частных производных часто опускаются, вместо них перед индексом, по которому производится дифференцирование, ставится точка с запятой «;» в случае ковариантной и запятая ", " в случае частной производной. Таким образом, выражение выше можно также записать как
и символы частных производных часто опускаются, вместо них перед индексом, по которому производится дифференцирование, ставится точка с запятой «;» в случае ковариантной и запятая ", " в случае частной производной. Таким образом, выражение выше можно также записать какЯвные выражения для символов Кристоффеля второго рода получаются, если сложить это уравнение и другие два уравнения, которые получаются циклической перестановкой индексов:
где
 — контравариантное представление метрики, которое есть матрица, обратная к
— контравариантное представление метрики, которое есть матрица, обратная к  , находится путём решения системы линейных уравнений
, находится путём решения системы линейных уравнений  .
.Связь с безындексными обозначениями
Формальные, безындексные определения связности абстрагируются от конкретной системы координат и поэтому более предпочтительны при доказательстве математических теорем.
Пусть X и Y — векторные поля с компонентами
 и
и  . Тогда k-я компонента ковариантной производной поля Y по отношению к X задается выражением
. Тогда k-я компонента ковариантной производной поля Y по отношению к X задается выражениемУсловие отсутствия кручения у связности, :
![\nabla_X Y - \nabla_Y X = [X,Y]\](d648cf4c00e22c528c0c716bfc400b2d.png) , эквивалентно симметричности символов Кристоффеля по двум нижним индексам:
, эквивалентно симметричности символов Кристоффеля по двум нижним индексам:Замена координат
Несмотря на то, что символы Кристоффеля записываются в тех же обозначениях, что и компоненты тензоров, они не являются тензорами, потому что не преобразуются как тензоры при переходе в новую систему координат. В частности, выбором координат в окрестности любой точки символы Кристоффеля могут быть локально сделаны равными нулю (или обратно ненулевыми), что невозможно для тензора.
При замене переменных
 на
на  , базисные векторы преобразуются ковариантно,
, базисные векторы преобразуются ковариантно,откуда следует формула преобразования символов Кристоффеля:
Черта означает систему координат y. Таким образом, символы Кристоффеля не преобразуются как тензор. Они представляют собой более сложный геометрический объект в касательном пространстве с нелинейным законом преобразования от одной системы координат к другой.
Примечание. Можно заметить, например, из определения, что первый индекс является тензорным, то есть по нему символы Кристоффеля преобразуются как тензор.
Символы Кристоффеля в различных системах координат
Пользуясь выражением символа через метрический тензор, либо преобразованием координат, можно получить значения их в любой системе координат. В механике и физике чаще всего используются ортогональные криволинейные системы координат. В этом случае символы Кристоффеля с равными коэффициентами выражаются через коэффициенты Ламе (диагональные элементы метрического тензора)
 , а все остальные равны нулю.
, а все остальные равны нулю.Символы Кристоффеля первого рода выражаются так:
 , при
, при  .
. .
.
Символы Кристоффеля второго рода:
 , при
, при  .
.
Ниже приведены значения для распространённых систем координат:
- В декартовой системе координат
 :
:  , поэтому ковариантная производная совпадает с частной производной.
, поэтому ковариантная производная совпадает с частной производной. - В цилиндрической системе координат
 :
:  ,
,  . Остальные равны нулю.
. Остальные равны нулю. - В сферической системе координат
 :
:  ,
,  ,
,  ,
,  ,
,  . Остальные равны нулю.
. Остальные равны нулю.
См. также
Другие величины, широко используемые в тензорном анализе
Литература
- Димитриенко Ю.И. Тензорное исчисление. — М.: Высшая школа, 2001. — 575 с. — ISBN 5-06-004155-7
- Победря Б.Е. Лекции по тензорному анализу. — Издательство Московского университета, 1974. — 206 с.
Ссылки
Категории:- Математические обозначения
- Риманова (и псевдориманова) геометрия
- Связность (математика)
Wikimedia Foundation. 2010.